
깜푸의 패스트캠퍼스 데이터분석 부트캠프 2주차 학습일지
비전공자도 할 수 있는 왕초보 기초 통계, 엑셀 데이터 탐색
기술 통계 (Descriptive statistics)
: 표본 자체의 속성을 파악하는데 중점을 둔 통계 분석 방법, 데이터를 요약하고 설명
추론 통계
: 추출한 표본의 통계량 관찰, 분석 기법을 활용하여 모집단을 추론하는 통계 분석 방법
: P-value 등을 활용하여 추론의 신뢰도를 확보한다

Will Cukierski. (2012). Titanic - Machine Learning from Disaster. Kaggle. https://kaggle.com/competitions/titanic
엑셀의 [데이터 분석 도구] - [기술 통계] 를 사용하여 만든 기술 통계량 데이터 차트
전체 표본의 요약 통계를 분석해준다
*분포를 확인할 때 함께 확인해야하는 수치
-분포의 중심 : 평균, 중위값, 최빈값 등.. (정보의 편향성이 클 경우, 평균보다는 중위값을 살펴보는 것이 유리하기때문)
-퍼짐 정도 : 분산, 표준편차, 사분위수, 변동계수
-분포의 모양(비대칭성) : 왜도, 첨도

Iris Species dataset. kaggle. http://www.kaggle.com/datasets/uciml/iris
boxplot을 사용하여 데이터의 이상치 (Outliers) 를 확인할 수 있다

Will Cukierski. (2012). Titanic - Machine Learning from Disaster. Kaggle. https://kaggle.com/competitions/titanic
피벗 테이블과 피벗 차트를 사용하여 엑셀 데이터의 변수 간의 상관 관계를 분석할 수 있다

Will Cukierski. (2012). Titanic - Machine Learning from Disaster. Kaggle. https://kaggle.com/competitions/titanic
[데이터 분석 도구] - [공분산 분석]
*공분산
: 두 개의 확률 변수의 선형 관계를 나타내는 값
: 변수의 스케일에 따라 표준편차가 같이 움직이므로 공분산도 같이 커진다
: 두 변수가 아무 관계없는 독립 변수일 때, 공분산 = 0
(각자 변수가 서로 영향받지않고 따로따로 움직이기때문에 독립적이므로 공분산 = 0)
: 그러나 공분산 = 0 일 때, 두 변수가 독립은 아닐 수 있다

Will Cukierski. (2012). Titanic - Machine Learning from Disaster. Kaggle. https://kaggle.com/competitions/titanic
[데이터 분석 도구] - [상관 분석]
상관계수 분석의 경우, 양수 음수 상관없이 수치의 절댓값이 1에 가까울 수록 강한 상관 관계를 가지므로
하이라이트 된 부분의 상관관계가 강하다는 것을 확인할 수 있다.
→ 스케일이 달라 공분산으로는 두 집단을 비교하기 어렵기 때문에 표준화해서 스케일을 균일하게 만든 후 상관계수를 사용한다
*기초통계량
1. 중심경향성: 데이터 분포의 중심을 보여주는 값
(최빈값MODE, 중앙값MEDIAN, 평균값AVERAGE으로 확인)
: 산술평균, 가중평균, 기하평균
2. 퍼짐정도: 자료가 얼마나 흩어져있고 얼마나 모여있는지를 보여주는 값
(분산VAR.P/S, 표준편차STD.P/S, 범위MAX-MIN, IQR으로 확인)
그러나, MAX-MIN으로 퍼짐정도를 살펴봤을 때 범위 내의 관측값 분포에 대한 정보를 알 수 없으며 극단치가 미치는 영향이 매우 크다)
3. 왜도: 분포의 좌우 비대칭성 정도
-양의 비대칭: 오른쪽 꼬리 분포
-음의 비대칭: 왼쪽 꼬리 분포

4. 첨도
: 분포의 뾰족한 정도, 양쪽 꼬리의 두터움 정도를 나타내는 값
: 편차가 큰 데이터가 많을수록 커짐
: 이상치에 많은 영향을 받는다

*변량: 자료의 수치, 즉 데이터의 값을 의미하는 용어
*계급: 변량을 일정한 간격으로 나눈 구간, 계급을 정할 때 변량의 최소, 최대를 고려함
*도수: 각 계급에 속하는 변량의 개수
*상대 도수: 각 계급에 속하는 변량의 비율
*도수분포표: 주어진 자료를 계급에 따라 나누고 도수를 조사하여 요약한 표

(예시) 도수분포표
range의 각 항목인 170~175, 175~180 과 같은 구간은 계급
각 계급의 value는 도수를 의미하며, rate는 각 계급에 속하는 변량의 비율인 상대 도수
*평균(mean)(산술평균): 변량의 합을 변량의 수로 나눈 값

*분산(variance) : 변량이 중심(평균)에서 얼마나 떨어져있는지를 보기 위한 통계량
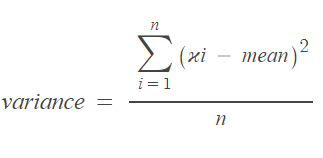
*편차(deviation) : 변량에서 평균을 뺀 값

*표준편차(standard deviation) : 분산의 제곱근, 관찰값들이 얼마나 흩어져 있는지를 하나의 수치로 나타냄, 관측된 변량의 스케일을 표준화할 수 있음

*확률 변수
: 일정한 확률을 갖고 일어나는 사건에 수치가 부여된 것
: 사건마다 부여된 확률 값을 변수로 나타낸 것
자료의 종류
1. 범주형 자료 (categorical, qualitative)
- 명목형 자료 : 순서가 없음 ex. 혈액형
- 순서형 자료 : 순서가 있음
ex) 차량 소 < 중< 대
ex) 만족도 1점 < 2점 < 3점 < 4점 < 5점
2. 양적 자료 (quantitative)
- 이산형 자료 ex. 동전을 10번 던졌을 때의 앞/뒤 횟수 분포 (확률변수가 정수로 끊어짐 INT)
- 연속형 자료 ex. 키, 몸무게 등 연속적인 숫자로 나타나는 것 (실수형 FLOAT)
→ 연송형 자료의 연속형 확률 분포는 정확한 값이 아니라 연속된 구간의 값을 나타내므로, 구간을 바탕으로 값을 구함
- 구간형 자료: 서로 비교하는 것이 의미있는 자료, but 서로의 비율이나 절대값은 의미없음 (사칙연산이 안됨)
ex. 기온 10도 < 30도 (30도가 3배 덥다고 분석하지않음)
ex. 1999년 < 2024년 < 2030년 (과거-미래의 연도 자체를 비교)
- 비율형 자료: 서로의 비율을 비교할 수 있음 (사칙연산 가능)
ex. 키, 몸무게 등..
ex. 로프의 길이가 10m < 20m (20m짜리가 10m보다 2배 길다고 비교할 수 있다)
통계적 데이터 분석 / 모델링
이동훈 강사님
*가설 검정
: 통계적 추론의 하나로서, 모집단 실제의 값이 얼마가 된다는 주장과 관련해, 표본의 정보를 사용해서 가설의 합당성 여부를 판정하는 과정
: "귀무가설이 옳다"는 전체 하에서 가설 검정이 이루어진다
: 귀무가설을 기각할 만한 충분한 증거가 제시되지않는 한 귀무가설은 기각되지않는다
ex. 재판에서 무죄 추정의 원칙이라는 전제하에서 재판이 이루어지며, 피고가 무죄가 아니라는 충분한 증거가 제시되지 않는 한 피고는 무죄이다
: 내가 주장하는 것은 대립가설이지만 검정의 대상이 되는 것은 귀무가
*귀무 가설(H0, 영 가설)
: 기본적으로 참으로 추정, 처음부터 버릴 것으로 예상하는 가설
(차이가 없거나, 의미있는 차이가 없는 경우)
: 등호(=)로 관계가 설정됨

*대립 가설(H1, 연구 가설)
: 귀무 가설에 대립하는 명제
: 귀무가설을 기각하는 반증의 과정을 거쳐 참이라고 받아들여질 수 있음
: 부등호(≠) 혹은 크기를 나타내는 (<) (>)를 사용하여 관계를 설정함
: 가설이 부등호로 나타날 경우 양측 검정. >,<로 나타날 경우 단측 검정

*P-value (유의 확률)
: 귀무 가설이 맞다는 전체 하에, 표본에서 실제로 관측된 통계치와 같거나 더 극단적인 통계치가 관측될 확률
: P-값이 작을수록 대립가설이 옳다고 추론할 수 있는 통계적 증거가 더 강하게 존재
: 일반적으로 5%의 유의수준을 기준으로 삼는다
: 5%의 유의수준(α)을 기준으로 봤을때, P-value ≤ α 이면 H0 이 기각되고 P-value > α 이면 기각되지않음
: 상관 계수 r 이나 결정 계수 r2 등의 지표를 함께 활용해 분석 결과를 더 정확히 표현할 수 있다
*t-test (t검정)
: 두 집단(또는 한 집단의 전,후)의 평균에 통계적으로 유의미한 차이가 있는지를 검정
: 적합한 t-test 방법을 선택하기 위한 F검정이 선행되어야 한다
: t-test의 귀무가설=두 집단의 평균에 유의미한 차이가 없다 (p > 유의수준α)
: t-test의 대립가설=두 집단의 평균에 유의미한 차이가 있다 (p < 유의수준α)
*F-검정
: 두 집단의 분산에 통계적으로 유의미한 차이가 있는지를 검정
: F-검정의 귀무가설=두 집단의 분산에 유의미한 차이가 없다 (p > 유의수준α)
: F-검정의 대립가설=두 집단의 분산에 유의미한 차이가 있다 (p < 유의수준α)


해당 문제를 해결하기 위해 한 집단의 전 후 를 비교하는 F검정 실시
[데이터] - [데이터 분석 도구] - [F-검정:분산에 대한 두 집단]
→ F 검정 결과 P-value가 0.05보다 작으므로, 두 집단의 분산에 유의미한 차이가 있음
→ 등분산 가정 t-test를 실시해야한다
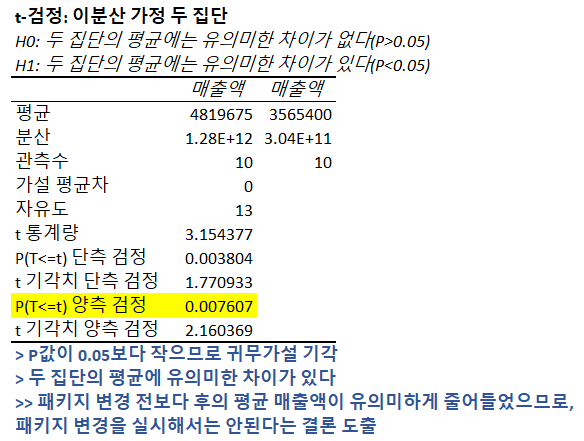
[데이터] - [데이터 분석 도구] - [t-검정: 등분산 가정 두 집단]
*회귀 분석
: 두 개 이상의 연속형 변수(수치)인 종속 변수와 독립 변수 간의 관계를 파악하는 분석
: 두 변수 간의 관계를 파악해 우리가 알고 싶은 값을 예측하는 것이 목적

y : 종속 변수, 우리가 알고 싶은 값 (우리가 통제할 수 없다는 특징)
x : 독립 변수, 우리가 알고 있는 값 (우리가 통제 가능하다는 것이 특징)
ex. 한 회사의 매출액과 광고비 사이의 관계를 알고 싶을 때
y는 매출액, x는 광고비에 대입할 수 있음
→ 광고비에 의한 매출 변화를 알고 싶은 것이므로
회귀 분석의 종류
- 선형 회귀 분석 : 함수식이 선형 함수 식일 때
- 단순 선형 회귀 분석 : 독립 변수 x 가 한 개
- 다중 선형 회귀 분석 : 독립 변수 x 가 여러 개
2. 비선형 회귀 분석 : 함수식이 선형 함수 식이 아닐 때
단순 선형 회귀 분석
: x와 y의 관계를 가장 잘 설명하는 직선, 직선 그래프로 나타남
: y와 x 사이의 1차 방정식 구하기
: (실제값-예측값)인 오차를 살폈을 때, 전체적으로 오차가 가장 작은 것
: 결정 계수로 설명력을 해석함




*결정 계수
: 0~1 값을 가지며 1에 가까울수록 회귀 모형이 실제 값을 잘 설명함
(1에 가까울수록 설명력이 높음을 의미)
*다중 선형 회귀 분석
: 독립 변수가 2개 이상일 때 독립 변수들과 종속 변수 간의 관계를 파악하는 분석
: 조정된 결정 계수로 설명력을 해석함 (1에 가까울수록 설명력이 높음을 의미)

변수들의 각각 P-값이 0.05보다 작으면 유의미한 영향을 미친다고 볼 수 있음
*회귀분석 로직
- 상관 분석으로 16개 이내의 상관 관계가 높은 변수 추출
- 모든 변수를 포함한 다중선형회귀분석
- 유의미한 변수들로만 다중선형회귀분석
- 유의미한 변수들을 각각 단순선형회귀분석
*시계열 데이터 분석
: 시간의 흐름에 따라 발생된 데이터를 분석하는 기법
: 정상 시계열 데이터 / 비정상 시계열 데이터로 구분된다
: 정상성 - 추세나 계절성을 가지고 있지 않으며, 관측된 시간에 무관한 성질
*지수 평활법
: 현재 시점에 가까운 시계열 자료에 큰 가중치를 주고, 과거 시계열 데이터일수록 작은 가중치를 주어 미래 시계열 데이터를 예측하는 기법
: 엑셀 함수 =FORECAST.ETS 로 예측할 수 있다

E열의 머리글은 '매출액'
F열의 머리글은 'FORECAST.ETS'
→ 실제 매출액과 예상 매출액의 열이 구분되어야 이후 차트에서 구분된다

*머신러닝
: 경험과 학습을 통해 자동으로 개선하는 컴퓨터 알고리즘의 연구이며 인공지능의 한 분야
- 지도 학습
: 정답(Y)이 있는 데이터를 활용, 분류(Classification), 회귀(Regration) 문제들을 해결할 수 있다
: 분류 - 2개 이상의 결과값으로 분류하는 지도 학습, 어떤 구간에 속하는지 분류하는 것으로 연구 방법으로 널리 사용됨 ex. 고객군 분류, 스팸 메일 여부 판단 등
: 회귀 - 특정한 1개의 결과값을 예측하는 지도 학습, 특정 값 하나를 정확히 예측해야하므로 분류보단 덜 사용됨 ex. 주가 예측, 기온 예측 등
- 비지도 학습
: 정답(Y)이 없는 데이터를 활용
- 강화 학습
: 학습 시스템의 행동에 보상 또는 벌점을 주어 가장 큰 보상을 받는 방향으로 유도하는 방법
: 가장 큰 보상을 얻기 위해 행동을 선택하는 방법을 정의하는 것을 정책이라고 한다
데이터 시각화 차트를 그릴때 어떤 숫자로 어떤 차트를 그릴지 선행적으로 고민해봐야한다
차트는 숫자 데이터로 인해 그려지기 때문에 어떤 숫자로 그릴 것인지, 어떤 차트가 숫자를 잘 설명할 것인지 생각해야한다

'패스트캠퍼스 BDA 13기' 카테고리의 다른 글
| [패스트캠퍼스 데이터 분석 부트캠프] 7주차_SQL 기초 문법 (0) | 2024.04.08 |
|---|---|
| [패스트캠퍼스 데이터 분석 부트캠프] 4주차_파이썬 제어문과 반복문(If문, While문, For문) (0) | 2024.04.08 |
| [패스트캠퍼스 데이터 분석 부트캠프] 3주차_파이썬Python 기초 문법 배우기- 자료형, 리스트, 튜플, 인덱싱 (1) | 2024.04.08 |
| [패스트캠퍼스 데이터 분석 부트캠프] 1주차_엑셀 데이터 분석 기초 (0) | 2024.04.08 |
| [패스트캠퍼스 데이터 분석 부트캠프] 1주차_OT (0) | 2024.04.08 |



